Halvledere er betegnelsen for en samling af elektroniske komponenter som alle har det til fælles at man kan styre strømmen i et kredsløb ved at tillade strøm at passere gennem dem eller undlade at lade strøm passere gennem dem. Med brugen af halvledere kan man lave bolsk algebra og det er en af grundpillerne i computeren som vi kender den.
For at forstå hvad en halvleder er så må vi først forstå hvordan strøm normalt løber gennem ledninger og andre almindelige ledere.
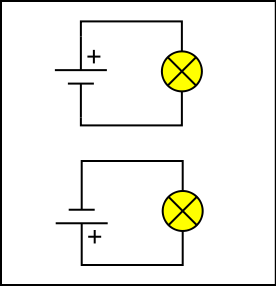
Hvis man sætter en almindelig glødepære til en jævnstrøms forsyning (f.eks. batteri e.l.) så vil den lyse uanset hvilken vej strømmen kommer ind som vist på figur 1. Den eneste måde af afbryde den på er at tage den ud af kredsløbet, enten fysisk eller med en kontakt som det kendes fra den almindelige strøm vi har i huse.
Dioden
Den simpleste halvleder der findes er dioden. Den kan ikke styres men tillader altid kun strømmen at gå en en retning. På figur 2 ses hvad der sker hvis man sætter en diode ind i jævnstrøms kredsløbet med en glødepære.
Som det ses så lyser pæren nu kun når strømmen har den ene retning hvor dioden virker som en leder men ikke i den anden retning hvor dioden ikke leder strøm.
Ved første øjekast ser det jo ikke særligt interessant ud, men med denne simple halvleder kan man lave en af grundpillerne i den bolske algebra.
Med to kontakter, to dioder og en modstand kan man lave en OR gate (eller kredsløb) eller en AND gate (Og kredsløb).
OR gate
Or gate kender man i en simpel form i husets el-installation der hvor man har to kontakter der kan tænde en lampe. Hvis bare en af dem er sluttet til så er lampen tændt.
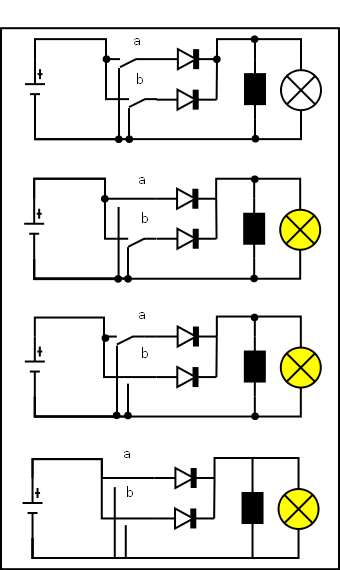
I computeren er det lidt mere kompliceret men princippet er det samme. Figur 3 viser en grundopsætning af en OR gate.
Det er vel ikke overraskende at når begge kontakter (a) og (b) er slukkede så er der ingen lys. Men hvorfor kortslutter (a) ikke bagom (b) når kontakt er tændt? Svaret er at dioden der sidder mellem afbryder (b) og pæren sikre at strømme ikke kan løbe den vej. Det er jo netop diodens opgave kun at lede strømmen fra plus til 0 (nul) i pilens retning og ikke lede den anden vej. Nå kontakt (b) er tændt og kontakt (a) er slukket sker der jo det samme ved at dioden ved konktakt (a) spærre for strømme. Når begge kontakter er tændt er der jo ingen steder hvor der ellers kunne lave en kortslutning og pæren lyser.
Vi kan altså nu sætte en sandhedstabel op for dette kredsløb som det bruges i den bolske algebra. Vi betragter slukket som falsk (0) og tændt som sand (1):
| a | b | Resultat |
| Falsk (0) | Falsk(0) | Falsk(0) |
| Falsk(0) | Sandt (1) | Sandt(1) |
| Sandt(1) | Falsk(0) | Sandt(1) |
| Sandt(1) | Sandt(1) | Sandt(1) |
Der arbejdes stadig på resten af indlæget